Mind over Data
Книга рассказывает о революции в научном методе. Она случилась благодаря простым диаграммам причинно-следственной связи в стиле точек и стрелочек. Это напрямую противоречит концепции “correlation doesn’t imply causation”, которая доминировала с конца 19 века. Основной ответ статистиков на это было, что корреляцию можно прослеживать только на значимых переменных. Как определить значимость переменной - непонятно. На этот вопрос есть два решения: do-нотация и counterfactuals. Работа с этими вещами происходит ровно на этих самых диаграммах.
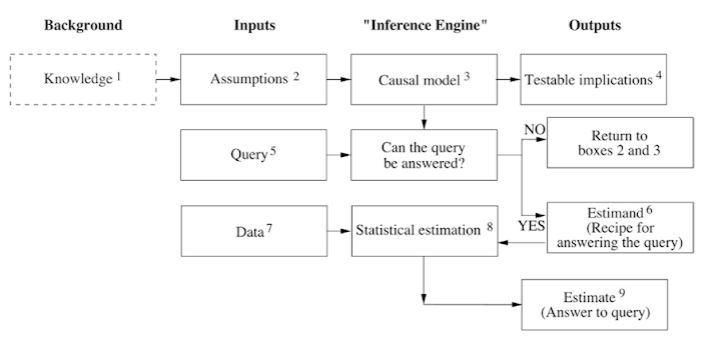
Прежде, чем переходить непосредственно к диаграммам причинности необходимо заглянуть в процесс “а как мы делаем выводы”. Для этого можно ввести машинку выводов/inference machine. Она состоит из трёх вводных: допущения/assumptions, запрос/query и данные/дата. Сначала мы должны решить можно ли в принципе ответить на запрос. Дальше мы конструируем рецепт/estimand для генерации ответа. И с помощью этого рецепта добавляя к нему ингридиенты данные мы можем дать ответ, и то приблизительный.
Разумные существа (и AI) могут понимать работу с причинами и следствиями (Casual model) на трёх разных уровнях. Это модель называется ladder of casuality:
- Seeing / Association - делаем выводы на основе данных, которые у нас есть.
- Doing / Intervention - выполняем действие для перехода в требуемое состояния.
- Imagining / Counterfactuals - представляем себе воображаемые миры для того, чтобы понять причину событий. Собственно, воображаемый аргумент - это и есть то что называют контрфактуалом/conterfactuals.
Самая первая диаграмма связей причины и следствия к исследованию окраса у морских свинок. Проблема была в игнорировании законов Грегоря Менделя при наследовании цвета окраса. В результате была выдвинута гипотеза о влиянии внешней среды на цвет. Для оценки влияния среды был проведён эксперимент, где в контрольной среде свинки оставили окраску своего родителя только в 3% случаях.
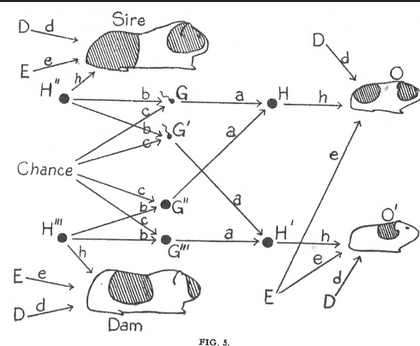
Sewall Wright’s first path diagram, illustrating the factors leading to coat color in guinea pigs. D = developmental factors (after conception, before birth), E = environmental factors (after birth), G = genetic factors from each individual parent, H = combined hereditary factors from both parents, O, _O_ʹ = offspring. The objective of analysis was to estimate the strength of the effects of D, E, H (written as d, e, h in the diagram). (Source: Sewall Wright, Proceedings of the National Academy of Sciences [1920], 320–332.)
В диаграммах есть три базовые комбинации: соединение, разветвление и коллайдер.
- A→B→C - соединение/junction. Пример: датчик пожара на основе дыма (огонь → дым → тревога). Если мы зафиксируем параметр B, то мы исключим влияние первопричины на наш вывод, например: закурив в комнате.
- A←B→C - разветвление/fork. Пример: корреляция между способностью читать и размером ноги у детей, где первопричиной является возраст. Это первый пример того, как связь параметров может дать бессмыслицу в причине, но успех в корреляции. Мы можем убрать её, если зафиксируем возраст ребёнка в данных и посмотрев что разницы никакой нет.
- A→B←C - коллайдер/collider. Пример: считаем что успех актёра зависит от таланта и красоты. Опасность такого сочетания в диаграмме в том, что если мы зафиксируем параметр B, то будем делать исключающие выводы. Успешный актёр без таланта будет считаться только из-за красоты, и наоборот. Что наводит на мысли о связи красоты и таланта, тогда как мы посмотрели только на половину нужной выборки и сделали себе неправильные допущения.
Из этих комбинаций складываются все диаграммы необходимые для исследования причинных связей. Знать эти комбинации нужно для того, чтобы правильно выбирать значимые переменные, которые можно или наоборот нельзя варьировать. Если мы не учитываем причинно-следственные связи, то порождаем в своём решения предвзятость/bias. И это только кубики для постройки более сложных вещей.
Рассмотрим парадокс Монти-Холла. В рамках этой игры за одной из трёх дверей есть автомобиль, и нам предлагают поменять своё решение после открытия одной из дверей. Внутренняя интуиция говорит о том, что шансы равны, но числа говорят об увеличении шансов на победу в случае смены. Происходит это по причине связи выбором двери ведущим и нашим выбором.
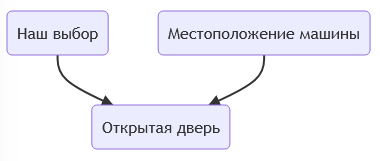
Фиксация на одном параметры в случае коллайдера создаёт в голове эффект исключающих выводов. И мы начинаем находить связь - там, где её нет.
Если мы поменяем правила игры и разрешим ведущему открыть любую дверь из двух оставшихся, то парадокса не будет. Именно так контрфактуалы работают с диаграммами Мы в своей голове воображаем потенциальные миры. Воображение можно свести к изменению стрелок в диаграмме и валидации полученной идеи на основе известного опыта. Основная проблема заключается в том, какие стрелки можно убирать, а какие нет.
Долгие дебаты касательно вреда курения состояли вокруг простого вопроса: было ли курение причиной для рака или была общая скрытая переменная. Статистически было известно, что шанс заболеть раком у курильщика был выше в 9 раз. При этом были и заболевшие из некурящих людей в виде 11% от общей выборки людей в рамках исследований. Допуская что общая причина генетика, мы можем сформулировать разницу в изменение одной стрелки в диаграмме.
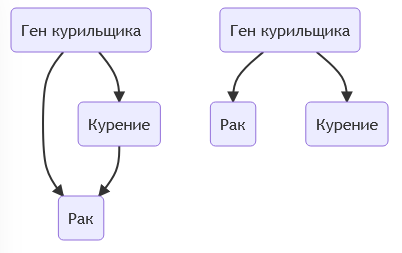
Допустим связь только через общую причину. Тогда результаты наших выборок, где в 9 раз больше курящих с раком должна приводить к наличию гена у 99% курильщиков. Если мы сможем это опровергнуть, то вывод останется только в наличии связи между курением и раком. Правда гораздо позже было открыто, что рак вызывают смолы и так же что есть ген отвечающий за восприимчивость к ним.
Допустим, что мы хотим провести исследование о том, как нам запускаться в новых городах. Для этого мы решили выбрать новый город, где будем проводить статистическое исследование и собрали данные из пяти предыдущих городов, где уже проводили разные типы исследований. На языке диаграмм мы провели следующие исследования:
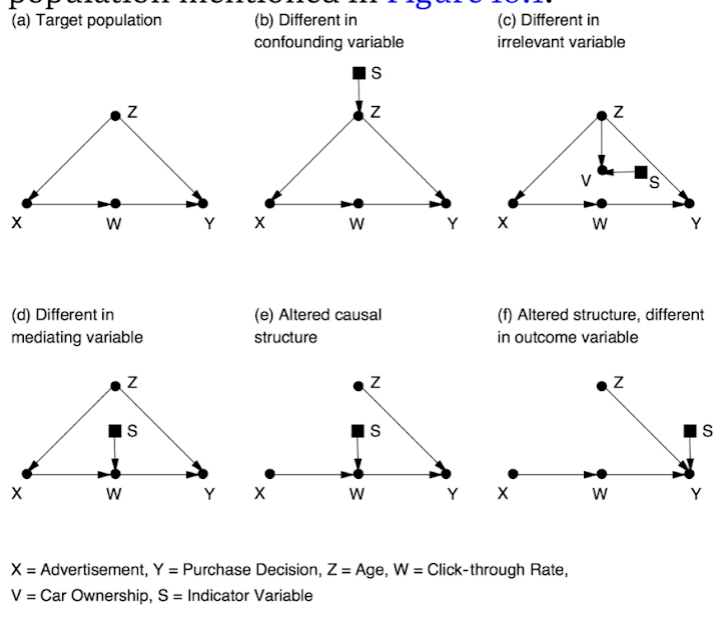
Город c - исследовался по независимой переменной, поэтому результаты его будут совпадать с нужным нам городом. Но мы не знаем насколько Z влияет на X и Y. С другой стороны исследование в городе e с помощью рандомизации выборки убрало связь между рекламой и возрастом, а фиксация на количестве кликов смогло показать связь между рекламой и покупкой. Если мы сможем посчитать эти факторы в нужном городе, то сможем ответить на свой вопрос. Что делать с оставшимися исследованиями? В случае города f, мы видим что на покупку влияет и реклама, и возраст. Взяв результаты из города e, мы можем попробовать дополнить наши результаты. Для этого в статистику была добавлена do-нотация. И сделала математика перевода do-нотаций в обычную теорию вероятности. С помощью неё в случае доказанных (точнее не опровергнутых) гипотез, мы можем давать себе качественные и количественные ответы в случае нескольких неполных/неправильных количественных исследований.
Если на этих примерах из книги стало интересно, то для погружения рекомендую прочитать первоисточник. За кадром остались такие приёмы, как: “backdoor test”, “frontdoor test”, и небольшое количество математики по do-calculus.